Trigonometry (from Greek trigonon "triangle" + metron "measure")

Want to learn Trigonometry? Here is a quick summary.
Follow the links for more, or go to Trigonometry Index

Trigonometry ... is all about triangles.

Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more!

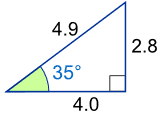
Right-Angled Triangle

The triangle of most interest is the right-angled triangle. The right angle is shown by the little box in the corner:

Another angle is often labeled θ, and the three sides are then called:

• Adjacent: adjacent (next to) the angle θ
• Opposite: opposite the angle θ
• and the longest side is the Hypotenuse

Why?

Why is this triangle so important?
Imagine we can measure along and up but want to know the direct distance and angle:

Or we have a distance and angle and need to "plot the dot" along and up:

Questions like these are common in engineering, computer animation and more.
And trigonometry gives the answers!

Sine, Cosine and Tangent

The main functions in trigonometry are Sine, Cosine and Tangent

They are simply one side of a right-angled triangle divided by another.

For any angle "θ":

(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.)

Example: What is the sine of 35°?

Using this triangle (lengths are only to one decimal place):

sin(35°) = OppositeHypotenuse = 2.84.9 = 0.57...

Calculators have sin, cos and tan, let's see how to use them:

Example: What is the missing height here?

• We know the Hypotenuse
• We want to know the Opposite

Sine is the ratio of Opposite / Hypotenuse:

sin(45°) = OppositeHypotenuse

Get a calculator, type in "45", then the "sin" key:

sin(45°) = 0.7071...

0.7071... is the ratio of the side lengths: in other words the Opposite is about 0.7071 times as long as the Hypotenuse.
Maybe you can figure out the height now?
But let's do it formally using some algebra:

Start with:sin(45°) = OppositeHypotenuse

Put in what we know:0.7071... = Opposite20

Swap sides:Opposite20 = 0.7071...

Multiply both sides by 20:Opposite = 0.7071... × 20

Calculate:Opposite = 14.14 (to 2 decimals)

Done!

Try Sin Cos and Tan

What are Real Numbers?

When both the rational and irrational numbers combined, the combination is defined as the real numbers. Real numbers can be both positive or negative, and they are denoted by the symbol “R”. Numbers like a natural number, decimals, and fraction comes under the real number.

Classification of Real Numbers

• Natural Numbers– It includes all the counting numbers such as 1, 2, 3, 4,…
• Whole Numbers– Numbers starting with zero are called whole numbers, like 0, 1, 2, 3, 4,…
• Integers– Whole numbers and negative of all natural numbers are collectively known as integers, for example -3, -2, -1, 0, 1, 2,
• Rational Numbers– All the numbers that can be written in the form of p/q, where $q\ne 0$ are known as Rational numbers.
• Irrational Numbers– The numbers which cannot be written in the form of p/q (simple fraction) are known as irrational numbers. Irrational numbers are non-terminating and non-repeating in nature.

Properties of real numbers

• Commutative property- If we have real numbers m,n. The general form will be m + n = n + m  for adaddition andmn = nm for multiplication
• Associative property- If we have real numbers m,n,r. The general form will be  m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication
• Distributive property- If we have real numbers m,n,r. The general form will be – m (n + r) = mn + mr and (m + n) r = mr + nr
• Identity property- For addition: m + (- m) = 0

In this page area of a quadrilateral we are going to see how to find the area in mensuration. First let us see the formulas to be used to find the area of any quadrilateral then we are going to see example problems and their properties. 

Formula:

Area of quadrilateral = (1/2)  x d x (h₁ + h₂)

Here d -diagonal

h₁ & h₂ - perpendicular heights

Definition of quadrilateral:

The word quadrilateral can be separated as Quad + lateral. Here quad means four and lateral means sides. A shape which is having four sides is generally called quadrilateral. The shapes parallelogram, rectangle, square, rhombus and trapeziums are one of the type of quadrilateral. 

Properties of quadrilateral:

• Sum of interior angles is 360°
• It has four sides
• It has four vertices 

Now we are going to some example problems based on these formulas

Example 1:

Find the area of a quadrilateral which is having the diagonal is measuring 50 m  and perpendicular height is measuring 10 m and 20 m

Solution:

Area of quadrilateral = (1/2)  x d x (h₁ + h₂)

Here h₁ = 10 m, h₂ = 20 m and d = 50 m

Area of quadrilateral = (1/2) x 50 x (10 + 20)

                            = (1/2) x 50 x 30

                            =  25 x 30  

                            = 750 m²

Matrix

In order to arrange numerous numbers, mathematics provides a simple solution: matrices. A matrix can be defined as a rectangular grid of numbers, symbols, and expressions arranged in rows and columns. These grids are usually charted by brackets around them.

The dimensions of a matrix are represented as R X C, where R is the number of rows and C is the number of columns. This R X C notation is also called the order of the matrix.

Types of Matrices

There are various types of matrices, depending on their structure. Let's explore the most common types:

Null Matrix

A matrix that has all 0 elements is called a null matrix. It can be of any order. For example, we could have a null matrix of the order 2 X 3. It's also a singular matrix, since it does not have an inverse and its determinant is 0.

Any matrix that does have an inverse can be called a regular matrix.

Row Matrix

A row matrix is a matrix with only one row. Its order would be 1 X C, where C is the number of columns. For example, here's a row matrix of the order 1 X 5:

Column Matrix

A column matrix is a matrix with only one column. It is represented by an order of R X 1, where R is the number of rows. Here's a column matrix of the order 3 X 1:

Square Matrix

A matrix where the number of rows is equal to the number of columns is called a square matrix. Here's a square matrix of the order 2 X 2:

Diagonal Matrix

A diagonal matrix is a square matrix where all the elements are 0 except for those in the diagonal from the top left corner to the bottom right corner. Let's take a look at a diagonal matrix of order 4 X 4:

A special type of diagonal matrix, where all the diagonal elements are equal is called a scalar matrix. We can see a 3 X 3 scalar matrix here:

A scalar matrix whose diagonal elements are all 1 is called a unit matrix, or identity matrix.

The matrix in mathematics is a rectangular or square array of numbers or variables, arranged in the form of rows and columns. Individual items in a matrix are known as elements or entries.

The size of the matrix is determined by some its rows and columns. Matrix with ‘m’ rows and ‘n’ columns is read as ‘m*n’ matrix where m and n are its dimensions.

$A=\left[\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\\ 9& 10& 11& 12\end{array}\right]$

For example ,the matrix A mentioned above  is a 3*4 matrix ,where 1,5,9,2,6 etc are its elements.

Matrices Problems

Two matrices can be added or subtracted element by element, provided both are of the same size.

Below image will help us in understanding the addition and subtraction operation on matrices,

But there is a rule for matrix multiplication, the number of columns in the first matrix should be equal to a number of rows in the second.

If A is a matrix of m*n and B is a matrix of n*p then their product matrix C=(A*B) will be m*p, whose elements are produced by the dot product of a corresponding row of A and a corresponding column of B.

The above image gives us a better understanding of multiplication of matrices.

Algebra - Basic Definitions

It may help you to read Introduction to Algebra first

What is an Equation

An equation says that two things are equal. It will have an equals sign "=" like this:

x

+

2

=

6

That equation says: what is on the left (x + 2) is equal to what is on the right (6)

So an equation is like a statement "this equals that"

Parts of an Equation

So people can talk about equations, there are names for different parts (better than saying "that thingy there"!)

Here we have an equation that says 4x − 7 equals 5, and all its parts:

A Variable is a symbol for a number we don't know yet. It is usually a letter like x or y.

A number on its own is called a Constant.

A Coefficient is a number used to multiply a variable (4x means 4 times x, so 4 is a coefficient)

Variables on their own (without a number next to them) actually have a coefficient of 1 (x is really 1x)

Sometimes a coefficient is a letter like a or b instead of a number:

Example: ax² + bx + c

• x is a variable
• a and b are coefficients
• c is a constant

An Operator is a symbol (such as +, ×, etc) that shows an operation (ie we want to do something with the values).

A Term is either a single number or a variable, or numbers and variables multiplied together.

An Expression is a group of terms (the terms are separated by + or − signs)

So, now we can say things like "that expression has only two terms", or "the second term is a constant", or even "are you sure the coefficient is really 4?"

Exponents

The exponent (such as the 2 in x2) says how many times to use the value in a multiplication. Examples: 82 = 8 × 8 = 64 y3 = y × y × y y2z = y × y × z

Exponents make it easier to write and use many multiplications

Example: y⁴z² is easier than y × y × y × y × z × z, or even yyyyzz

Polynomial

Example of a Polynomial: 3x² + x - 2

A polynomial can have constants, variables and the exponents 0,1,2,3,...

But it never has division by a variable.

Monomial, Binomial, Trinomial

Can trigonometry be used in everyday life?

Trigonometry may not have its direct applications in solving practical issues, but it is used in various things that we enjoy so much. For example music, as you know sound travels in waves and this pattern though not as regular as a sine or cosine function, is still useful in developing computer music. A computer cannot obviously listen to and comprehend music as we do, so computers represent it mathematically by its constituent sound waves. And this means sound engineers need to know at least the basics of trigonometry. And the good music that these sound engineers produce is used to calm us from our hectic, stress full life – All thanks to trigonometry.

Trigonometry can be used to measure the height of a building or mountains:

if you know the distance from where you observe the building and the angle of elevation you can easily find the height of the building. Similarly, if you have the value of one side and the angle of depression from the top of the building you can find and another side in the triangle, all you need to know is one side and angle of the triangle.

Trigonometry in video games:

Have you ever played the game, Mario? When you see him so smoothly glide over the road blocks. He doesn’t really jump straight along the Y axis, it is a slightly curved path or a parabolic path that he takes to tackle the obstacles on his way. Trigonometry helps Mario jump over these obstacles. As you know Gaming industry is all about IT and computers and hence Trigonometry is of equal importance for these engineers.

Trigonometry in construction:

In construction we need trigonometry to calculate the following:

• Measuring fields, lots and areas;
• Making walls parallel and perpendicular;
• Installing ceramic tiles;
• Roof inclination;
• The height of the building, the width length etc. and the many other such things where it becomes necessary to use trigonometry.

Architects use trigonometry to calculate structural load, roof slopes, ground surfaces and many other aspects, including sun shading and light angles.

Trigonometry in flight engineering:

Flight engineers have to take in account their speed, distance, and direction along with the speed and direction of the wind. The wind plays an important role in how and when a plane will arrive where ever needed this is solved using vectors to create a triangle using trigonometry to solve. For example, if a plane is travelling at 234 mph, 45 degrees N of E, and there is a wind blowing due south at 20 mph. Trigonometry will help to solve for that third side of your triangle which will lead the plane in the right direction, the plane will actually travel with the force of wind added on to its course.

Trigonometry in physics:

In physics, trigonometry is used to find the components of vectors, model the mechanics of waves (both physical and electromagnetic) and oscillations, sum the strength of fields, and use dot and cross products. Even in projectile motion you have a lot of application of trigonometry.