In this page area of a quadrilateral we are going to see how to find the area in mensuration. First let us see the formulas to be used to find the area of any quadrilateral then we are going to see example problems and their properties. 

Formula:

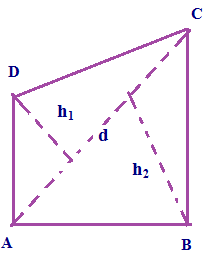
Area of quadrilateral = (1/2)  x d x (h₁ + h₂)

Here d -diagonal

h₁ & h₂ - perpendicular heights

Definition of quadrilateral:

The word quadrilateral can be separated as Quad + lateral. Here quad means four and lateral means sides. A shape which is having four sides is generally called quadrilateral. The shapes parallelogram, rectangle, square, rhombus and trapeziums are one of the type of quadrilateral. 

Properties of quadrilateral:

• Sum of interior angles is 360°
• It has four sides
• It has four vertices 

Now we are going to some example problems based on these formulas

Example 1:

Find the area of a quadrilateral which is having the diagonal is measuring 50 m  and perpendicular height is measuring 10 m and 20 m

Solution:

Area of quadrilateral = (1/2)  x d x (h₁ + h₂)

Here h₁ = 10 m, h₂ = 20 m and d = 50 m

Area of quadrilateral = (1/2) x 50 x (10 + 20)

                            = (1/2) x 50 x 30

                            =  25 x 30  

                            = 750 m²

Matrix

In order to arrange numerous numbers, mathematics provides a simple solution: matrices. A matrix can be defined as a rectangular grid of numbers, symbols, and expressions arranged in rows and columns. These grids are usually charted by brackets around them.

The dimensions of a matrix are represented as R X C, where R is the number of rows and C is the number of columns. This R X C notation is also called the order of the matrix.

Types of Matrices

There are various types of matrices, depending on their structure. Let's explore the most common types:

Null Matrix

A matrix that has all 0 elements is called a null matrix. It can be of any order. For example, we could have a null matrix of the order 2 X 3. It's also a singular matrix, since it does not have an inverse and its determinant is 0.

Any matrix that does have an inverse can be called a regular matrix.

Row Matrix

A row matrix is a matrix with only one row. Its order would be 1 X C, where C is the number of columns. For example, here's a row matrix of the order 1 X 5:

Column Matrix

A column matrix is a matrix with only one column. It is represented by an order of R X 1, where R is the number of rows. Here's a column matrix of the order 3 X 1:

Square Matrix

A matrix where the number of rows is equal to the number of columns is called a square matrix. Here's a square matrix of the order 2 X 2:

Diagonal Matrix

A diagonal matrix is a square matrix where all the elements are 0 except for those in the diagonal from the top left corner to the bottom right corner. Let's take a look at a diagonal matrix of order 4 X 4:

A special type of diagonal matrix, where all the diagonal elements are equal is called a scalar matrix. We can see a 3 X 3 scalar matrix here:

A scalar matrix whose diagonal elements are all 1 is called a unit matrix, or identity matrix.

The matrix in mathematics is a rectangular or square array of numbers or variables, arranged in the form of rows and columns. Individual items in a matrix are known as elements or entries.

The size of the matrix is determined by some its rows and columns. Matrix with ‘m’ rows and ‘n’ columns is read as ‘m*n’ matrix where m and n are its dimensions.

$A=\left[\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\\ 9& 10& 11& 12\end{array}\right]$

For example ,the matrix A mentioned above  is a 3*4 matrix ,where 1,5,9,2,6 etc are its elements.

Matrices Problems

Two matrices can be added or subtracted element by element, provided both are of the same size.

Below image will help us in understanding the addition and subtraction operation on matrices,

But there is a rule for matrix multiplication, the number of columns in the first matrix should be equal to a number of rows in the second.

If A is a matrix of m*n and B is a matrix of n*p then their product matrix C=(A*B) will be m*p, whose elements are produced by the dot product of a corresponding row of A and a corresponding column of B.

The above image gives us a better understanding of multiplication of matrices.